Сортировка элементов массива

ИНФОРМАТИКА   |   Последнее обновление 11.10. 2024 Admin   |  

Рассмотрим метод сортировки данных, который называ­ется пузырьковой сортировкой (также его называют методом обмена).

Будет приведен алгоритм и его реализация на языке программирования Python.
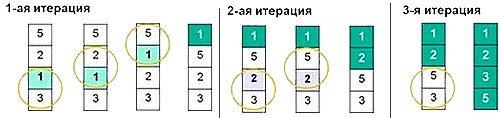
Упорядоченный массив создается на том же участке памяти, где находится исходная последовательность. Идея метода состоит в том, чтобы попарно сравнивать соседние элементы.
Каждый проход начинается с начала последовательности. Первый элемент массива сравнивается со вторым, если поря­док между ними нарушается, то они меняются местами. Затем сравниваются второй с третьим, третий с четвертым и так далее: элементы с неправильным порядком в паре меняются местами до конца массива. В итоге после первого прохода, максимальный(или минимальный, в зависимости от вида сортировки: по возрастанию/по убыванию) элемент будет находиться на последнем месте в массиве, он как бы «всплывет» наверх. Именно поэтому этот метод называется пузырьковой сортировкой. На следую­щем проходе рассматривается последовательность от 1 до N-1, затем от 1 до N-2 и так до конца. После каждого прохода можно проверять, выполнялись ли перестановки элементов. Если не выполнялись, то сортировка завершена.

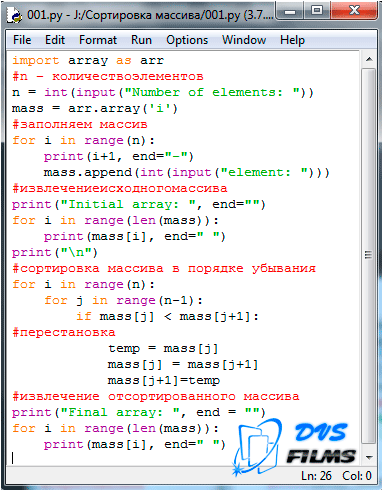
Задание 1. Реализация алгоритма сортировки на языке программирования Python.

ПО возрастанию:

my_list = [2,6,9,1,3,7,4]
a = sorted(my_list)
print(a)

По убыванию:

my_list = [2,6,9,1,3,7,4]
a = sorted(my_list, reverse = True)
print(a)

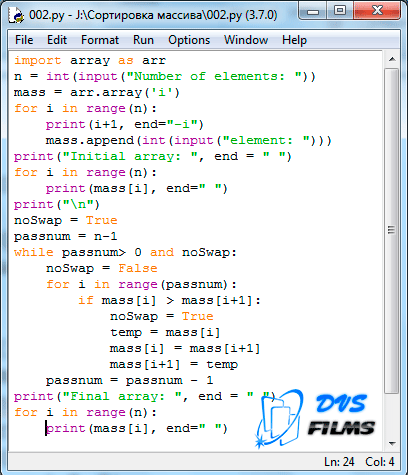
Задание 2. Пример консольной программы на языке программирования Python, которая считывает массив, сортирует его пузырьковым методом и выводит результат на экран.

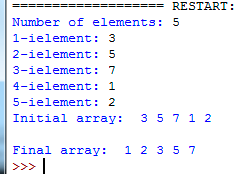Разберем код программы. Подключим необходимые библиотеки (строка 1), предложим пользователю ввести число N(количество элементов в массиве) и считаем число N(строка 3), создаем массив (строка 4), предложим пользователю ввести элементы массива и считаем элементы массива (строки 6-8), выполним сортировку пузырьковым методом (строки 16-26), выведем отсортированный массив на экран (29-31). Работа программы представлена на скриншоте.

Задание 3. (Для самостоятельного решения). Данатаблица плотности твердых тел. Расставьте значения плотности в порядке возрастания: S={22500, 2600, 900, 8900, 21500,2700,1100,240,19300}.

Сортировка в задачах ЕГЭ

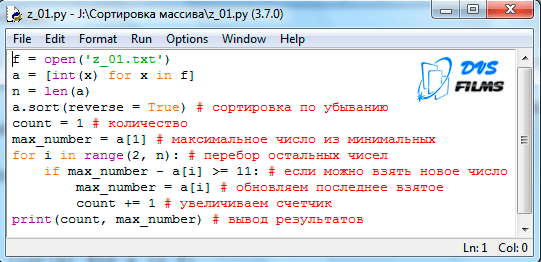
Z_01. «В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 11 единиц меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Входные данные
В первой строке входного файла находится число N – количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке. Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы.
При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32».
Файлы можно найти здесь.

Z_02. «В лесничестве саженцы сосны высадили параллельными рядами, которые пронумерованы идущими подряд натуральными числами. Растения в каждом ряду пронумерованы натуральными числами начиная с единицы.
По данным аэрофотосъёмки известно, в каких рядах и на каких местах растения не прижились. Найдите ряд с наибольшим номером, в котором есть ровно 13 идущих подряд свободных мест для посадки новых сосен, таких, что непосредственно слева и справа от них в том же ряду растут сосны. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: наибольший номер ряда и наименьший номер места для посадки из числа найденных в этом ряду подходящих последовательностей из 13 свободных мест.
Входные данные
В первой строке входного файла находится число N – количество прижившихся саженцев сосны (натуральное число, не превышающее 20 000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 100 000: номер ряда и номер места в этом ряду, на котором растёт деревце.
Выходные данные
Два целых неотрицательных числа: наибольший номер ряда и наименьший номер места в выбранной последовательности из 13 мест, подходящих для посадки новых сосен.
Типовой пример организации входных данных
7
40 3
40 7
60 33
50 125
50 129
50 68
50 72
Для приведённого примера, при условии, что необходимо 3 свободных места, ответом является пара чисел: 50; 69».

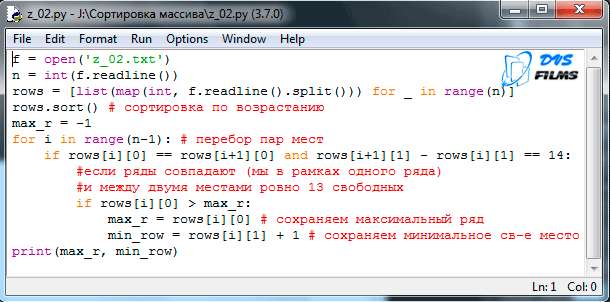Здесь мы тоже сортируем ряды и места в них, а после проходимся по всем идущим подряд парам и проверяем, чтобы ряды совпадали, а разница между соседствующими номерами мест была равна 14. И находим наибольший подходящий ряд и наименьшее в нем место.